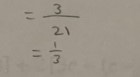Oopsy Daisy ... didn't mean make that error on math I know ...
How to catch those oopsies, slip-ups, careless, frustrating, I didn't mean to do that error.
Oops ... didn't mean to do that! Oopsy Daisy!
I’ve always wondered who this famous Daisy was 😆. I mean why isn’t it oopsy Fred or oopsy Diane? Why did Daisy get all the accolades?
Umm … squirrel! Where was I? Oh yeah, about those oopsies, slip-ups, careless, frustrating, I didn't mean to do that error. Here’s the lowdown on those, as they’re stealing marks from you and can be very bothersome 😡😠!
When your test mark is lower than your level of understanding
If you think of every Math by Edison post as a chapter in a book, then …
P.S. Want some error practice?
Here's what Daisy says about making errors on math you know?
It's annoying to make an error on math you know.
And on a test, it's doubly frustrating as your mark will not reflect your level of understanding. Today, I'll teach you an error strategy that will have you catch errors on math you know
– aka careless errors, slip-up errors, avoidable errors,
I can't believe I did that
Stupid mistake
Oops error
What did I do?
Oh no … what just happened?
Didn't plan on doing that … crap!
Noooooooo …
Oopsy Daisy!
When your test mark is lower than your level of understanding
If you get a mark of 75% on a test and lose 10% of your mark to errors on math that you know, that means you’re an ‘85%’ student with a 75% mark. Get 45% on a test and lose 20% of your marks on those “What did I do?” errors? That means you understood 65% of the test but didn’t get a 65! In that case are you a 45% or a 65% student? I’d say 65%, but your self-talk may say otherwise (Why am I making these mistakes?), and your confidence may be battered (Why can’t I do better?). What can you do?
You don’t plan to make those errors. Or do you?
Five reasons you make errors on math you know, and I’m certain you’re aware of the first four:
#1 Rushing (e.g. feeling the pressure of a timed test).
#2 Not reading the question carefully.
#3 Skipping steps.
#4 Not checking your work.
#5 Nervousness on a test (or test anxiety).
There’s a strategy to solve each of these obstacles. The first four are habits-driven, and the fifth requires specific coaching. Today, I’ll focus on, #4 ‘checking your work’ because, because, because it’s one habit that solves four - Solves #1, 2, 3 and 4. A four-for-one deal!
More on #4, the check
The ‘double-check is the famous directive given by parents, guardians and teachers to check your work, and it involves re-reading your work to catch errors. It’s a solution for some students but not the solution for most, as it takes too long. Plus, your teacher won’t have factored in time on a test for double-checking all questions.
The doublecheck is a solution for some students, but not the solution for most students.
Be me for a moment
You’re a learning strategist, and you work with teenagers and math, many of whom don’t like math or don’t feel they’re good at math. How would you solve this error problem? In other words, put yourself in my shoes and ask yourself this: 1) What strategy can I develop for a student to catch those errors? and 2) Where will their motivation come from to do this extra work? Welcome to my job - working with math students to solve any problem, with the objective that when they leave the session, they can replicate the strategy and solve problems on their own. They’re becoming independent and autonomous math students. But I digress.
What strategy can I develop for a student to catch those errors?
Here’s the strategy I teach students
Three guidelines to checking your work: 1. Do it differently, 2. Make sure it’s quick, and 3. It’s got to be easy. Different-quick-easy!
Exhibit A:
For the question, Evaluate 2 x 3, you write five as the answer. 2 x 3 = 5. Yes, I have seen grade 7s to grade 12 students write this, and university students make that error. Here’s the challenge to you: how can you check that 2 x 3 = 5 is wrong differently than how you did it? I’ll give you some time to think about it, and if you’re thinking, ‘It’s wrong, Edison”, I’ll respond with, “Yeah, I know.” But you didn’t know it was wrong when you made it on the test.
But you didn’t know it was wrong when you made it on the test.
Important: You’re not redoing the question, as that’s a double-check; you’re aiming to verify it’s wrong by checking a different way. Different being the operative word. Back to that question, check that 2 x 3 = 5 is wrong in a different way. Did you come up with a strategy to show it’s wrong? Wonderful! Hooray. Keep it up! You can never have enough acknowledgement when it comes to math. Bravo … had to sneak that one in. Magnificent! Ok, that’s the last one.
I have three questions for you:
1. Was it quick to do?
2. Was it easy to do?
3. Was it different?
If yes, to all three, then welcome, welcome to the wide, wonderful world of using a different check to catch those “Nooooooooo …” careless errors.
Yeah, I know, this post has been dragging on, I need to get to the point. But before I do one more thing, yeah, I know I heard that groan; give yourself a pat on the back, a high-five to self, as you figured out a different check on your own. Yay! ON YOUR OWN! That’s called INDEPENDENT learning!!!
Three ways to check that 2 x 3 = 5 is wrong
#1 Most common is to do the opposite or reverse operation of multiply (x), which is division. So to check whether 2 x 3 = 5 is right or wrong, you do 5 /3 (aka 5 divided by 3*), which isn’t 2. The answer of 5 is wrong.
Note: This is similar to checking that 2 x 3 = 6 is right as you’d do 6/3 (6 divided by 3), which is 2, so the answer of 6 is right.
*You may have used another symbol for division, called obelus - it’s the one that has a horizontal line with a dot above and below. Yeah, good old obelus – the symbol everyone knows and uses, but few know its given name. Sad, but true.
#2 You can use the meaning of the math symbol, x (math word is multiply), which means repeated addition. Then 2 x 3 becomes 3 + 3, which is 6. So, the 5 answer is incorrect.
#3 And that symbol x (called multiply or times) also means groups of, which tells us how to do it visually. Means that 2 x 3 can be made into a picture of two groups of three, lll lll, which gives 6. The answer of 5 is not correct, incorrect, not right, wrong!
If you think of every Math by Edison post as a chapter in a book, then …
Strategies #1 and #2 go back to the meaning of the Symbols, = and x (aka multiply).
And #3 goes back to doing math with a Picture. The Word, Evaluate, has a meaning, though, that’s not as effective an error check in this question.
I teach students how to do a different check for every question they do! It becomes exhilarating to catch errors when doing homework w/o always looking at the answers at the back of the textbook. Feels good to find these errors on a test!
Make error checking a habit, and you’ll be doing your future self a favour, and it is tests where you’ll see the benefits as “Oh no” errors get found and fixed, and reduced 😊!! Plus, you’ll be helping your teacher grimace less and slow down their onset of grey hair, as those errors are distressing to see, and mark.
This is a different take on the mantra ‘learning from your mistakes’ as you learn now, rather than later.
Review
Checking to find errors on math you know, that’s quick, easy and different, isn’t taught in schools. I know, it should be, right?
Students, you can find the check in the meaning of the math word, symbol or picture. Parents, this is a terrific way to ‘help’ your child reduce their careless errors (and yeah, I’d expect their motivation for your help on this to be higher). And teachers, have fun with it and make it into a game - finding errors is a lot more interesting than making errors.
Edison
Edison Hopkinson BSc Mech Eng, B. Ed
Learning strategist for math students
Strategies that have to work when the usual error ones don’t!
P.S.
Want some error practice?
Yes, no! Okay, are you sure? The future you won’t be happy with the present you, especially if you’ve made this error** before or someone you know has (sibling, parent, cousin, uncle, grandparent, ancestors, friend, classmate, teacher, coach …).
**Here’s the error: For the question, Evaluate 1/2 + 1/3 prove that 2/5 is wrong. 1/2 + 1/3 = 2/5. Yup that’s the ever-popular adding fractions and the most common math mistake made.
Hint-clue-tip: Use the meaning of the math Symbols (+, / or =) or make a picture. If you can’t find one message or email me.